Casimir
Naar de homepageABOUT CASIMIR
Topological quantities flow (article in Nature Physics by Leiden postdoc Caio et al.)
[21-01-2019]
We are used to ascribe properties to objects, such as color, temperature and phase—gaseous, liquid or solid. We can do this for each tiny part of any artifact. If someone asks about a specific point on the surface of a donut, you will tell them it’s brown, solid and at room temperature. Topological properties are different. They contain information about the entire object. For instance, a donut has one hole. It is impossible to count the amount of holes by focusing on a specific part of the donut. You need to consider it as a whole. Topology has proven to be important in many scientific fields. In 2016, for example, work on topology was recognized with the Nobel Prize in Physics.
Chern index
The so-called Chern index is another, albeit very abstract, topological quantity. This is a special case in topology. Recently it was discovered that the Chern index has a density—called Chern marker. This can tell you about the topology of an entire system even by just looking at the local level. The solid line in figure 1 shows the spatial distribution of Chern marker, where each local point has its own value. (Note that this graph would make no sense for a global property like the number of holes in an object.) The local points do however need to abide by one rule at the global level: the average of all local values should always be zero.
Topological current
Leiden physicist Marcello Caio, together with a team of scientists from the United Kingdom, has now discovered that if you perturb a system, the local Chern values will distribute by flowing from the boundaries toward the interior of the system. In contrast, global topological properties are robust against perturbations—the number of holes in a donut only changes after a big bite. In figure 1, a perturbation causes the graph to reshape to keep honoring the requirement that its integral should be zero. Caio and his colleagues discovered that this doesn’t happen instantaneously, so there must be a flow of Chern marker through the system. This constitutes topological current, in analogy to a conventional electric current.
Novel devices
Caio: ‘In the far future, this could enable the development of novel devices based on topological currents beside electric currents. There are many venues for research in this direction. Are there other ways to create this current? Can we steer them? There are many exciting possibilities.’
Publication
M. D. Caio, G. Möller, N. R. Cooper, and M. J. Bhaseen, ‘Topological Marker Currents in Chern Insulators’, Nature Physics
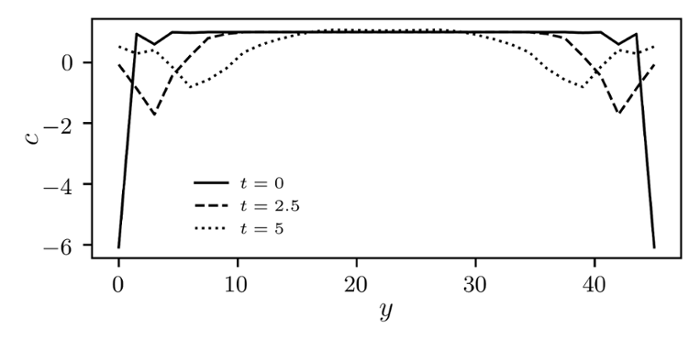 Three graphs for the spatial distribution (y) of Chern marker (c) at different times. The solid line shows the initial state when a small perturbation takes place at the edges. The two dashed lines show the distribution of Chern marker after some time. It is clear that the perturbation flows (non-instantaneously) to the middle. That means we are looking at a topological current.
Three graphs for the spatial distribution (y) of Chern marker (c) at different times. The solid line shows the initial state when a small perturbation takes place at the edges. The two dashed lines show the distribution of Chern marker after some time. It is clear that the perturbation flows (non-instantaneously) to the middle. That means we are looking at a topological current.